Understanding the Problem

Today's challenge revolves around determining the inverse Laplace transform of a specific function. The task at hand is to uncover the inverse Laplace transform, denoted as L^(-1){F(s)}.

Photo by Artur Aldyrkhanov on Unsplash

The Approach to the Solution

Addressing this problem is akin to tackling integral calculations. Just as there are fundamental integrals that everyone should memorize, certain techniques—like integration by parts and substitution—are essential tools in your toolkit. When it comes to finding inverse Laplace transforms, the same principle applies; familiarity with a few basic transforms and techniques is crucial.

One vital transform to remember is:

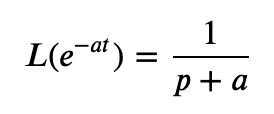
This transform stems from applying the Laplace shifting theorem to the constant function 1. If we instead consider:

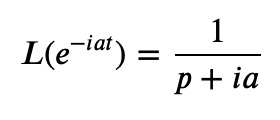
we can manipulate the denominator to become real:

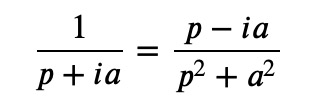
Furthermore, due to the linearity of the Laplace transform, we can derive from Euler’s formula:

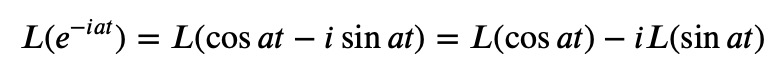
By analyzing both the real and imaginary components, we find:

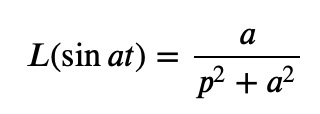
For the case when s=1, we have made notable advancements in determining our L^(-1){F(s)}:

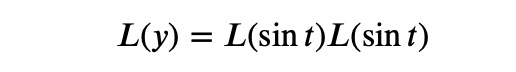
Utilizing the Convolution Theorem

Next, we can leverage the well-known convolution theorem, which applies to both Fourier and Laplace transforms. This theorem states that for two functions, f(t) and g(t), with their corresponding Laplace transforms F(s) and G(s), the following identity holds true:

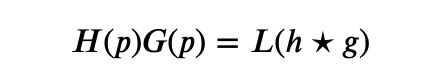
Here, the star symbol indicates the convolution operation:

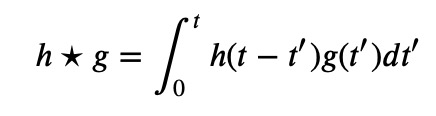
Thus, our task reduces to calculating the convolution of sin(t) with itself. Let's proceed with that:

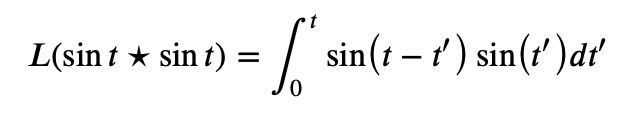
To make progress, we should apply a trigonometric addition formula. I can't recall it off the top of my head, so let's derive it quickly:

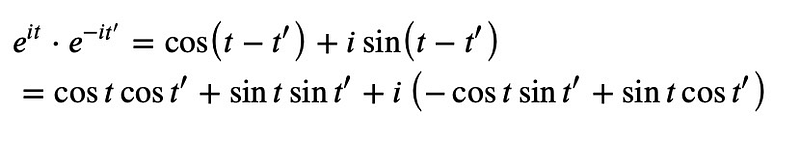
By comparing the real and imaginary components, we arrive at:

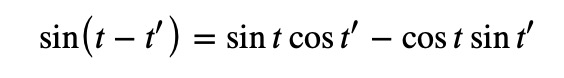
Now, we can insert this into the integral:

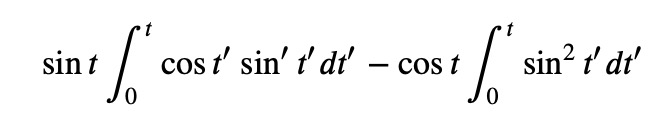
Both integrals can be evaluated using integration by parts:

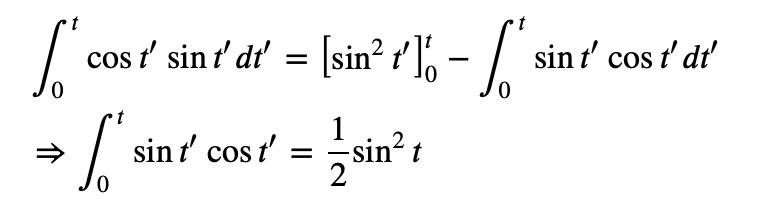
and

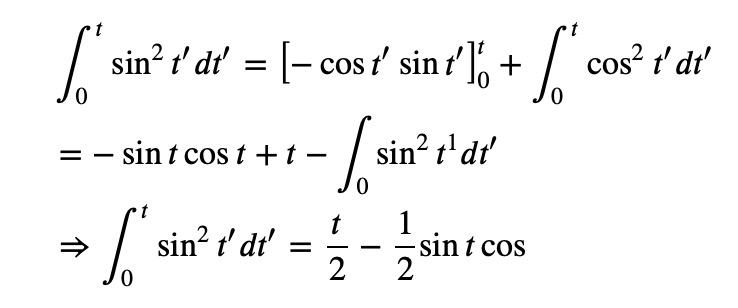
Compiling our findings yields:

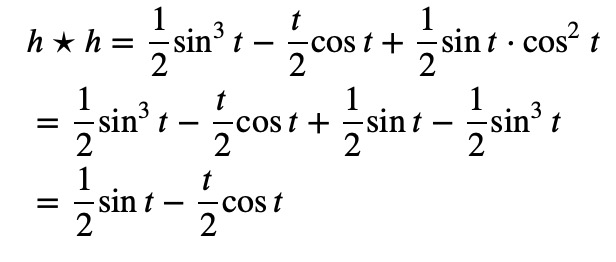
Conclusively, the inverse Laplace transform of:

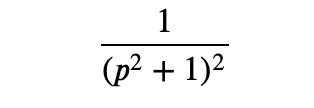
is:

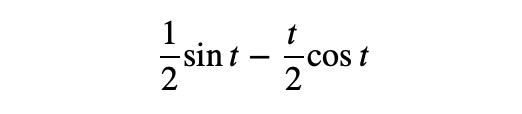
This video illustrates the Inverse Laplace Transform with examples and highlights key theorems vital for mastering the topic.

In this tutorial, learn how to compute the Inverse Laplace Transform of the function (s + 4)/(s^2 + 4s + 8), detailing step-by-step methods.