Plain Calculations

Initially, we have a basic equation to work through:

Here, multiplying the unknowns results in a value of 1, indicating that one of the variables must equal 1. Alternatively, if one variable were to equal 0, it would lead to inconsistencies in the puzzle's constraints, so we maintain that this variable equals 1.

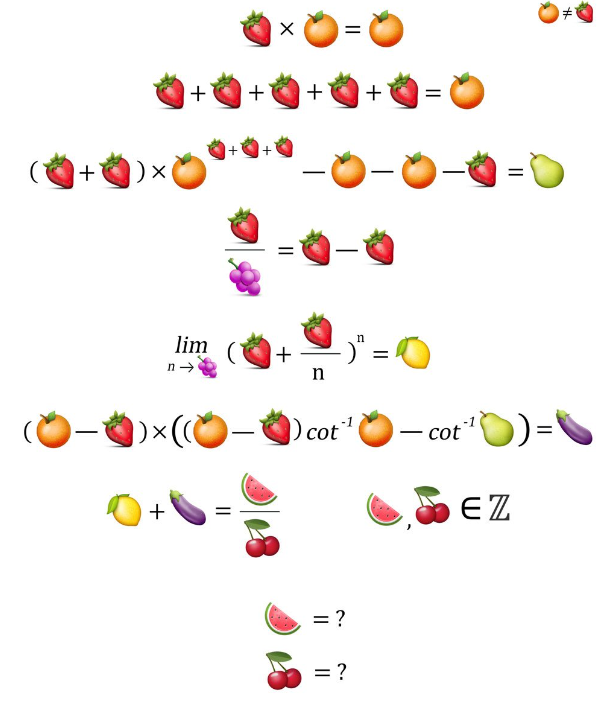
Next, we have:

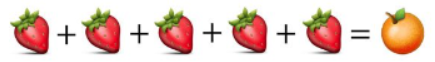
This leads us to conclude that 1 + 1 + 1 + 1 + 1 sums up to 5.

The complexity increases as we substitute our known values:

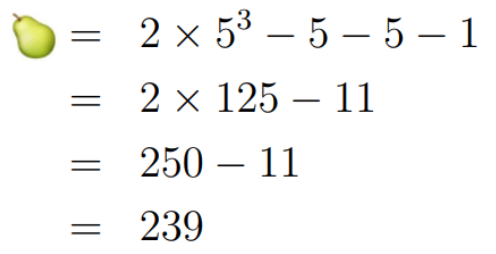
Introducing Infinity

The next equation introduces a peculiar concept:

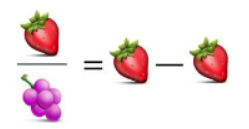
Given that one variable equals 1, we must determine what value divided by 1 results in 0:

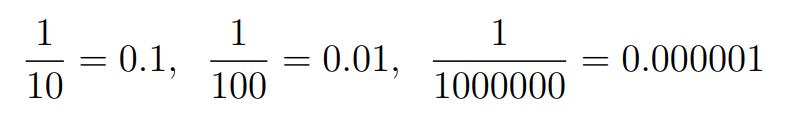
The more significant the variable, the closer we get to our target. Consequently, we tentatively set one variable to infinity.

Entering Calculus

Now, we must navigate a limit situation:

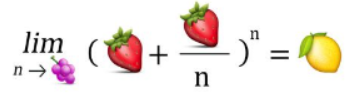
This is why we required the previous variable to be infinity! Substituting the fruit variables back into the equation gives us:

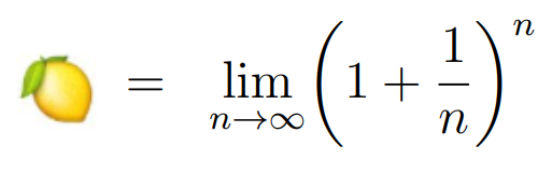
As n increases towards infinity, the expression nears a specific value, known as the limit of the expression as n approaches infinity. To visualize this better, we can experiment with increasingly larger values of n.

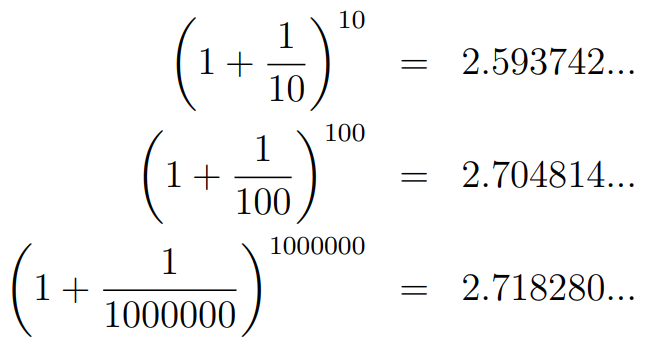
This expression converges towards Euler's number, denoted as e, a vital constant in mathematics, which we will now represent with a lemon.

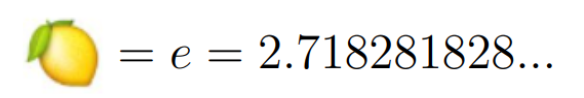
Entering Trigonometry

The following line of the puzzle presents:

This segment requires a lengthy calculation, but with the aid of a calculator, it becomes manageable. Before diving in, it's essential to understand the cotangent function, defined as the reciprocal of the tangent:

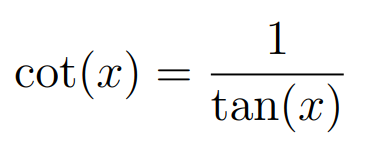
The cotangent in our puzzle has an exponent of -1, indicating it’s the inverse function of cot. Let's remember that one of our earlier variables equals 239. We can now substitute all our fruit values and solve for the eggplant:

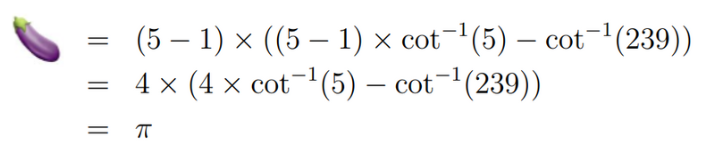
Final Stretch

At last, we arrive at:

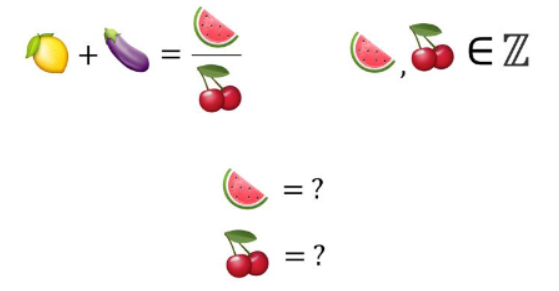
Recall that e equals approximately 2.71828, and the other variable represents pi at about 3.14159. We aim to express e + pi as a fraction of integers, but both e and pi are irrational numbers, and whether their sum is also irrational remains an unsolved question.

In summary, this puzzle likely originated on Reddit, where users often employ approximations to tackle such math challenges:

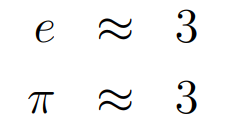
Using these methods, we can compute the values for our variables:

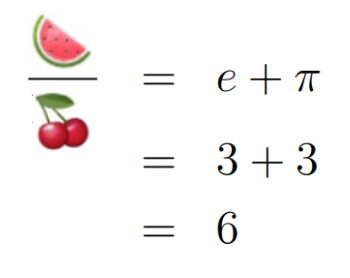
Thus, expressed as a fraction, we find that 6 equals 6/1, completing our puzzle:

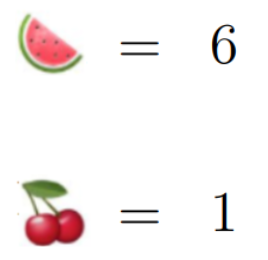
Now, having tackled this intricate puzzle, you should feel more equipped to approach any fruit math challenges that come your way!

Explore the first video titled "Fruit Logic Puzzle | Math Puzzles | Example 1" for a detailed explanation of similar mathematical puzzles.

Check out the second video, "Can you Guess the Price of the Pear? Riddle and Solution," to enhance your riddle-solving skills!