Chapter 1: Weekly Math Games Overview

This past week at Math Games was relatively quiet, with only four submissions. However, that’s perfectly fine, as it suggests that everyone is enjoying their summer away from their screens—at least, I hope that’s the case!

Let's congratulate this week's top competitors:

1st Place: Wotsit with 7 points 🎉

2nd Place: Jonathan Lynn Harvey with 5 points 🎉

3rd Place: Carl Reiner Holdt with 3 points 🎉

Other Participants: Göran Åhlander with 1 point 🎉

Here’s the solution 📝

To begin, let’s examine the diagram below.

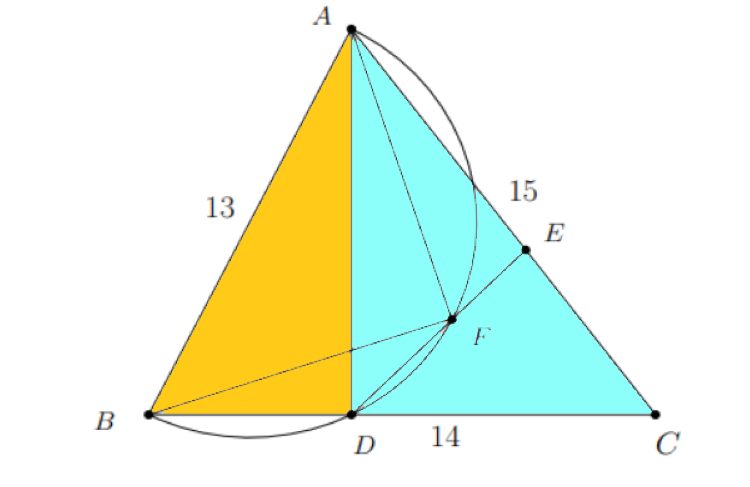
Take note of the two right-angled triangles, ABD and ACD, which I have highlighted in color. The crucial step is to employ Pythagoras’ Theorem for both triangles, keeping in mind the common side AD.

We know that AB = 13, AC = 15, and BC = 14. Therefore, we can express CD as 14 - BD. This information allows us to form an equation where BD is the only variable.

Now, solving for BD will also lead us to find CD and AD:

• BD = 5
• CD = 9
• AD = 12

Next, we will use the properties of similar triangles AED and ADC.

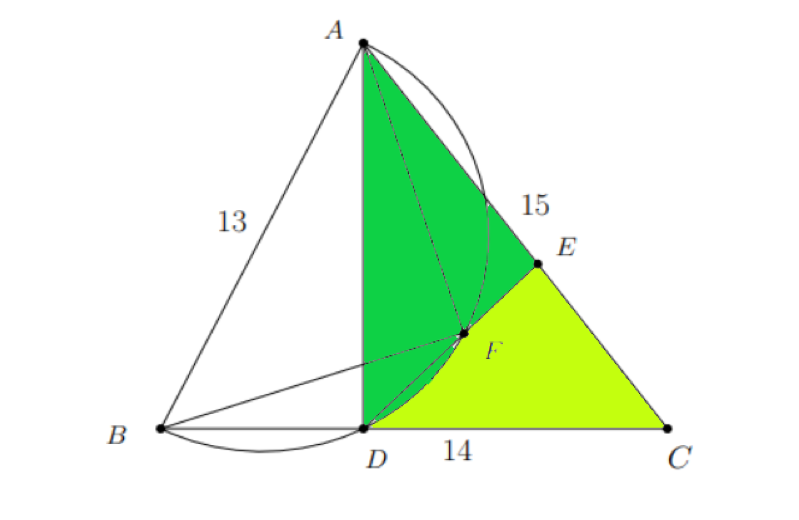
We can now establish the following ratios:

From this, we find AE = 48/5 and DE = 36/5.

The final stage of our solution begins with the two right angles AFB and ADB.

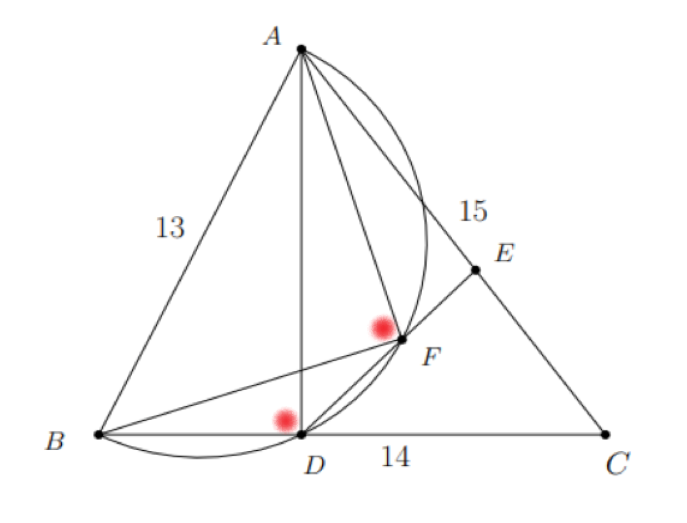
These angles are both 90 degrees, as the problem states that AD is perpendicular to BC and AF is perpendicular to BF. Since both right angles touch the circumference of the semicircle, quadrilateral ABDF must be cyclic.

In cyclic quadrilaterals, the sum of opposite angles equals 180 degrees. Thus, we have angle ABD + AFD = 180, which leads to angle ABD = angle AFE. Therefore, triangles ABD and AFE are similar, allowing us to set up the following ratios:

Recalling that AE = 48/5, we find FE = 4. Consequently, DF can be calculated as DE - FE.

Finally, we arrive at m + n = 16 + 5 = 21. Thus, the answer is B.

How did you fare in this week’s Math Games? Looking forward to seeing you all next week, challengers!

This video titled "Mn • MN definition" explores the mathematical definitions and implications of the terms involved.

In this video, titled "What is 'Minnesota Nice'?", the concept of social niceness in Minnesota is discussed, providing a cultural context to understanding mathematical problems in a friendly environment.