Understanding the Importance of Euler's Number in Growth
Written on
Chapter 1: The Significance of Euler's Number
Euler's number, approximately 2.71828, is intrinsically linked to natural processes of growth and decay. Whether discussing population dynamics or the returns on investments, mathematical models often incorporate 'e' to accurately represent these phenomena.
When I first encountered this concept in high school, I accepted it without question. However, as I've matured, I’ve come to understand the value of inquiry. This led me to ponder several questions:
- Why do we utilize 'e'?
- Why must it specifically be the constant valued at ‘2.718281828459045…’?
- Why can't we simply use another constant like '2', '3', or '10'?
It turns out there are compelling reasons for the preference of Euler's number. Not only do these reasons validate its usage, but they also highlight why 'e' stands out as one of the most vital constants in mathematics.
In this discussion, I will provide a brief historical overview of 'e' and investigate the rationale behind its application in modeling growth and decay. Additionally, I will touch upon some unique characteristics associated with this constant.
If you share my fascination with Euler's number, you will find this exploration both enlightening and engaging. Let’s dive in!
The Historical Journey of Euler’s Number
Surprisingly, Euler's number is a relatively recent addition to mathematics compared to constants like π. The earliest reference to this constant can be found in an appendix to John Napier’s logarithmic work from 1618, which was likely penned by William Oughtred. However, this mention did not explicitly acknowledge the constant.
A few years later, in 1624, Henry Briggs provided a numerical estimate of the base 10 logarithm of 'e', though he did not formally recognize it. In 1647, Saint-Vincent calculated the area under a rectangular hyperbola but failed to connect it to logarithms, thus overlooking 'e'.
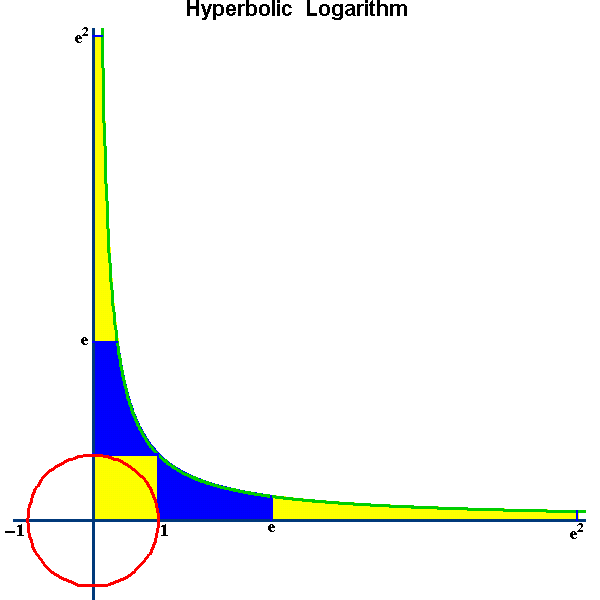
In 1661, Christiaan Huygens discovered a curve he termed “logarithmic,” which we now refer to as the “exponential curve” represented by the equation y = k*(a)^x. Huygens recognized the link between the rectangular hyperbola and logarithmic concepts, yet the number 'e' remained unacknowledged.
In 1668, Nicolaus Mercator published Logarithmotechnica, which introduced the concept of the "natural logarithm" while calculating logarithms based on 'e', although the constant itself was not named.
The Unexpected Discovery
In 1683, Jacob Bernoulli examined compound interest and demonstrated that the value of [1+(1/n)]^n lies between 2 and 3 as n approaches infinity, marking the initial approximation of 'e'.
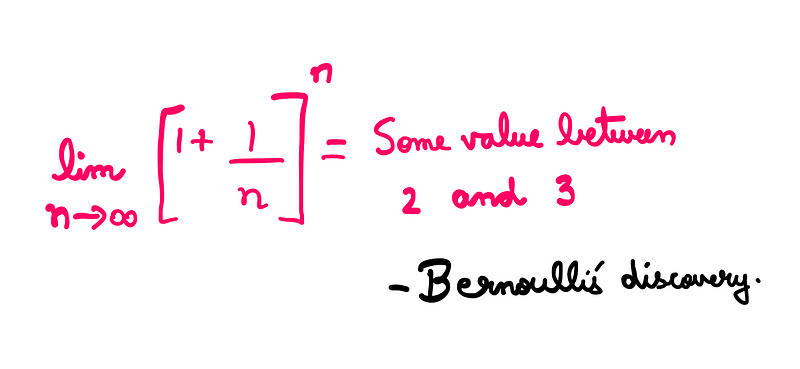
While one might expect 'e' to be identified through its logarithmic relationships, its first approximation arose through growth calculations, a surprising twist in its discovery.
By 1731, 'e' was formally identified in a letter from Leonhard Euler to Christian Goldbach. In 1748, Euler published Introductio in Analysin infinitorum, offering a comprehensive examination of his ideas surrounding 'e', including its factorial expressions and continued fractions. He also calculated its value to 18 decimal places without disclosing his methods.

Many contemporary mathematical notations can be traced back to Euler's work, making it unsurprising that his notation for 'e' became widely accepted. However, the rationale behind his choice of the letter 'e' remains a mystery, with theories suggesting it may relate to his surname or simply follow the alphabetical sequence.
Now that we've reviewed the historical context of 'e', let's examine what sets it apart from other mathematical constants.
Why Is Euler’s Number Unique?
Most notable constants in mathematics, such as π and √2, have long histories rooted in their geometric significance. In contrast, Euler's number emerged from its relevance to growth and decay, a concept that has garnered human interest relatively recently compared to geometry.
Consequently, it is understandable that 'e' is a newcomer in the mathematical landscape. Its significance is particularly evident in the field of calculus, which we will explore next.
What If We Used '2' Instead of Euler’s Number (e)?
The initial questions posed earlier were:
- Why do we use 'e'?
- Why is it necessary for it to be a constant valued at ‘2.718281828459045…’?
- Why can't it be another constant such as '2', '3', or '10'?
To investigate this, I will consider '2' as a growth constant and analyze the outcomes.
Let's plot 2^x:
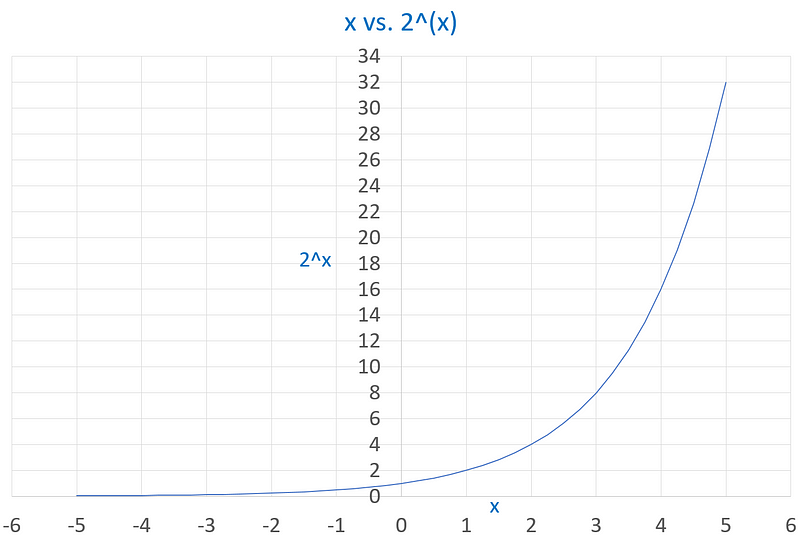
At first glance, this graph appears to depict exponential growth. If we interpret this as representing population growth over time, it seems that the population doubles at each interval.
However, growth in nature is inherently continuous, necessitating a mathematical approach that reflects this reality. Transitioning to calculus leads us to the following results:
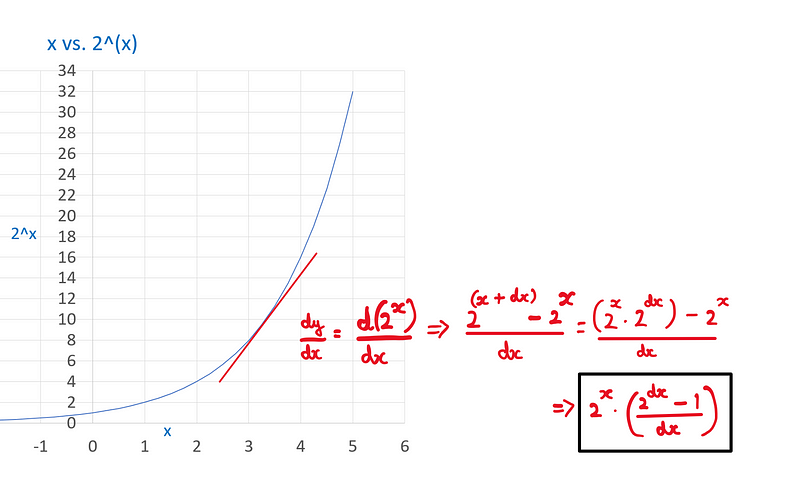
The findings illustrate that the rate of change of the function 2^x is contingent upon itself, influenced by a constant multiplier.
Generalizing the Result
We can generalize our findings as follows:
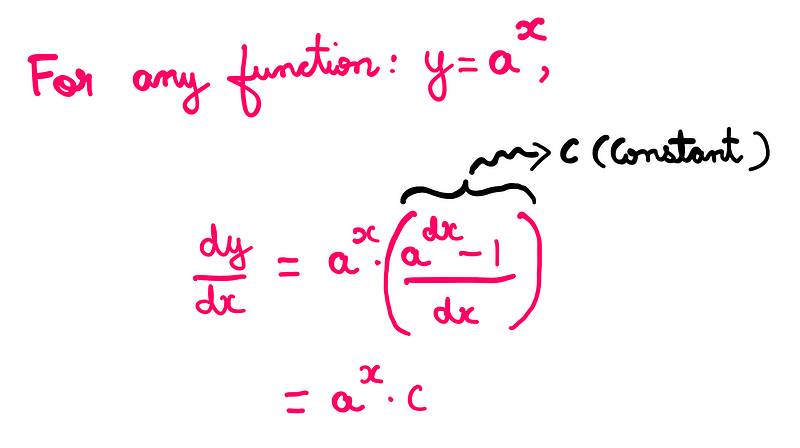
In fact, there is nothing inherently special about the number 2. Different base values yield different constant factors:
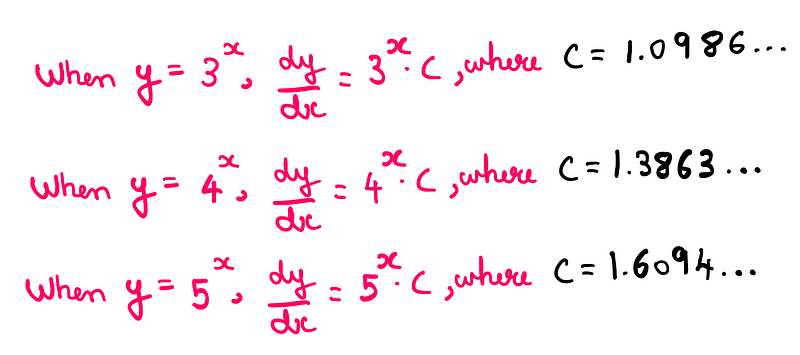
When we require the constant factor to equal 1, Euler’s number naturally emerges:
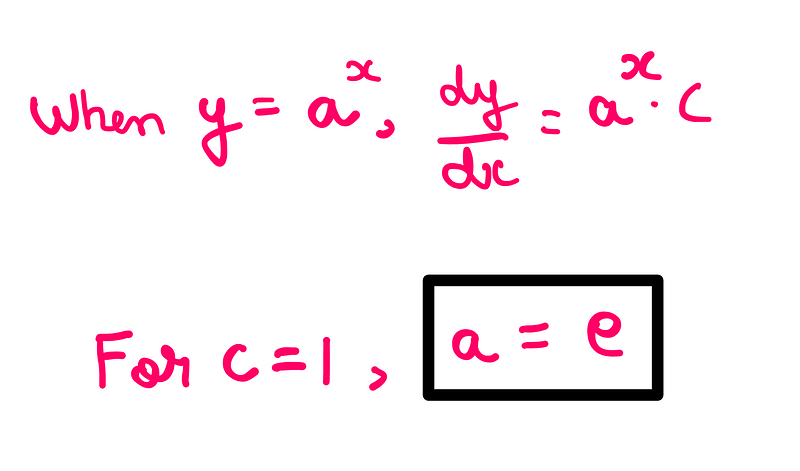
Thus, the factors linked to different numbers correspond to their natural logarithms:
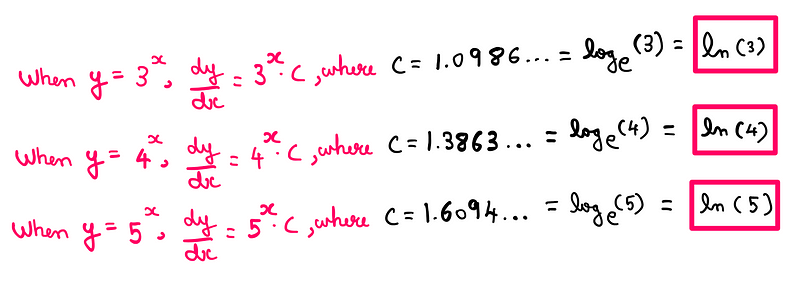
This leads to further fascinating aspects of Euler's number.
Significant Properties of Euler’s Number
When 'e' serves as the base for an exponential function (y = e^x), a unique characteristic emerges: the derivative of the function at any point is equal to the function itself. This is a distinctive property exclusive to this function:
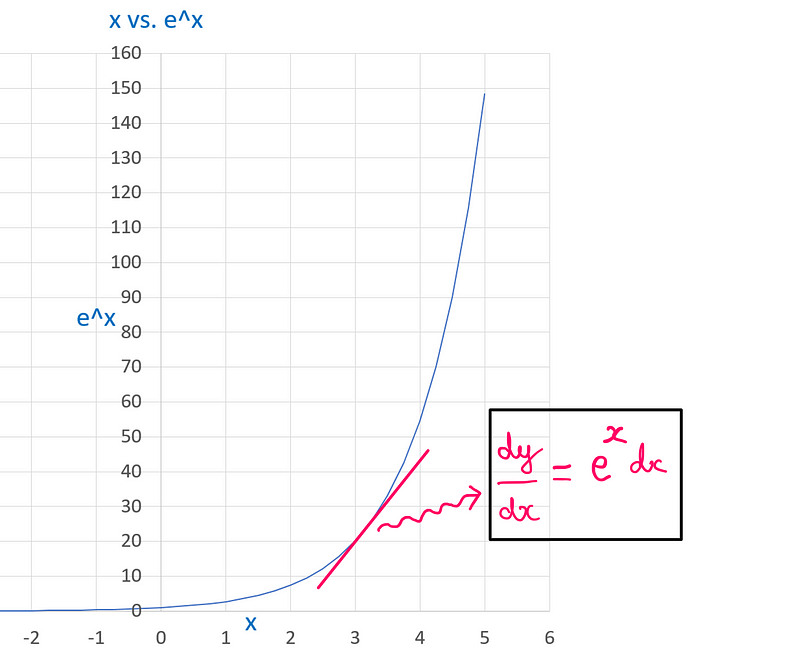
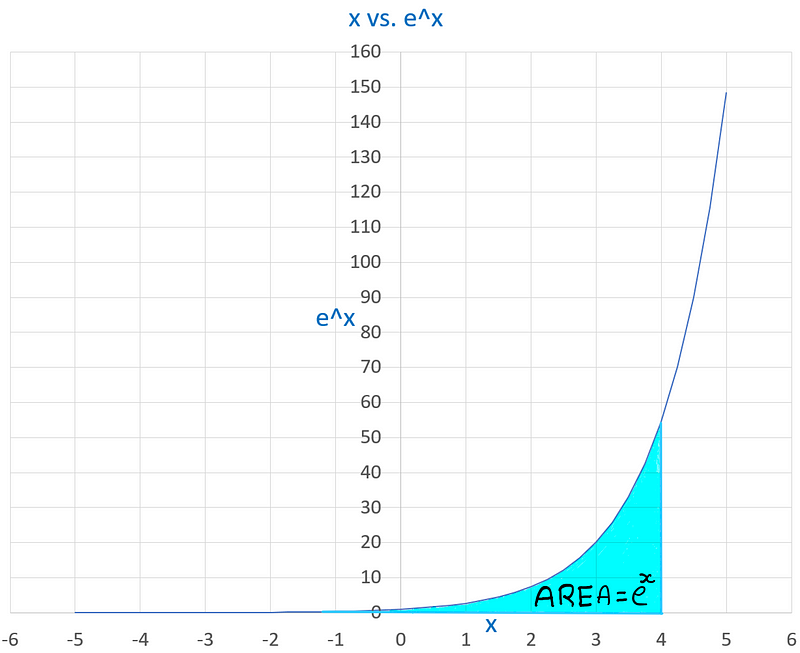
Moreover, the area under the curve for the function e^x at any right-hand limit of x equals the function's value, an invaluable property in integral calculus.
These attributes make 'e' the optimal base for analyzing growth and decay across various disciplines, including physics and biology.
Final Thoughts
In simpler terms, 'e' represents the maximum potential value for a continuously compounding growth function at a 100% growth rate over a single time period.
Euler's number serves as a fundamental measure for growth and decay in the natural world. While other constants can be used for similar equations, they often complicate the mathematics unnecessarily.
Employing Euler’s number introduces elegance and simplicity into these calculations. Given that we are part of the natural world ourselves, it’s no surprise that we are drawn to such innate elegance and beauty!
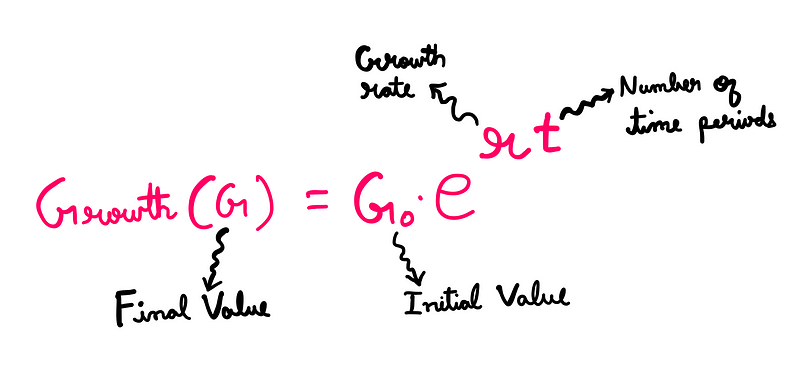
For further insights into this topic, consider watching these informative videos:
This video titled "Exponential Growth and Euler" explores the principles of exponential growth and the significance of Euler's number in mathematics.
In "What's so special about Euler's number e? | Chapter 5, Essence of calculus", the unique properties of 'e' are discussed in detail.
I hope this article was enlightening and informative. If you enjoyed it, consider showing your support by liking, following, or subscribing.