The Harmonious Intersection of Bach, Mathematics, and Music
Written on
Chapter 1: The Fusion of Music and Mathematics
Albert Einstein once mused, “If I were not a physicist, I would probably be a musician. I often think in music. I live my daydreams in music. I see my life in terms of music.” This sentiment reflects a long-standing belief in the Western world, originating from Pythagoras, that music and mathematics share a deep connection. This connection is evident in the mathematical principles that underlie musical sound production, scale formation, rhythms, and sometimes even composition.

Einstein as a Musician
The intriguing relationship lies in how musical and mathematical thinking intersect. Both disciplines are distinct languages that require years of dedication to master. They share a fundamental appreciation for recognizing patterns. Whether one is a composer, an improviser, a mathematician, or a physicist, the exploration of patterns is essential to uncovering what follows.
Bach, a virtuoso in musical composition, employed mathematical concepts in his craft. While he was not a mathematician per se, his thinking mirrored that of one. He adeptly used geometric operations to investigate melodies—employing techniques such as transposition, inversion, and retrograde inversion that parallel classical geometry. His exceptional talent lay in weaving these mathematical transformations into his music in innovative and artistic ways.
One of the extraordinary aspects of Bach's work is his ability to express fundamental mathematical ideas through music. A prime example is his “Crab Canon” from The Musical Offering, which showcases his playful and inventive use of mathematics. The composition features a single melody that creates a beautiful counterpoint when reversed. An engaging animation by Jos Leys illustrates this concept by transforming the score into a Möbius strip:
Chapter 2: Bach's Music and Fractal Geometry
Bach's work is not only a reflection of classical geometry but also exhibits characteristics of fractal geometry. His compositions serve as fertile ground for research in this field, revealing intricate patterns that resonate through his music.

Examining the Bourrée from his Cello Suite No. 3, we find a self-similar structure. The initial eight measures can be broken down into two short two-measure phrases followed by a longer four-measure phrase. Upon further analysis, one of the two-measure phrases reveals a similar structure, demonstrating a recursive pattern that extends throughout the piece.
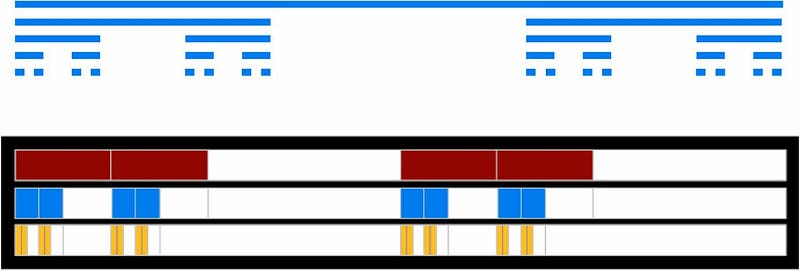
The visual representation of a Cantor comb illustrates self-similar patterns repeating at various scales, analogous to the distribution of note durations in a 16-measure excerpt from Bach's Cello Suite No. 3. Though the piece traditionally includes a repeat in the second section, it is often performed without it. This allows us to interpret the opening measures as a repeated short section followed by a longer one, further emphasizing the self-similar structure in the phrasing.
Bach and Cantor: Unveiling Fractals in Music
“It’s easy to play any musical instrument: all you have to do is touch the right key at the right time…”
www.cantorsparadise.com
Bach's music is rife with examples of self-similarity, from the intervallic scaling in his cello suites to his inventions and flute partitas. His Contrapunctus IX from The Art of Fugue also displays signs of intervallic scaling. Enthusiasts of Bach often describe his music as embodying endless spirals or wave-like circles, evoking the infinite detail found in the famous Mandelbrot set. An animation pairing Bach's Contrapunctus IX with a zoom into the Mandelbrot set showcases this captivating concept:
Conclusion: The Timelessness of Mathematics and Music
Mathematics possesses a timeless quality—Euler's identity remains just as beautiful and profound today as it was in 1748. The same can be said for the works of mathematicians like Archimedes, Newton, Gauss, and Einstein. Similarly, Bach's music transcends time, embodying a clarity and enduring charm. The great polymath Gottfried Wilhelm Leibniz once stated, “Music is the pleasure the human mind experiences from counting without being aware that it is counting.” In this light, listening to Bach allows us to delve deeper into the world of mathematics.
Thank you for reading! If you found this exploration engaging, please show your appreciation by clicking the “Applause” icon below. You can also subscribe for the latest updates directly to your inbox.
Further Resources
[1] My “Bach & friends” interview featuring the Emerson String Quartet
[2] Fractal geometry of music
[3] Intervallic scaling in the Bach Cello Suites
[4] Hunting fractals in the music of J. S. Bach (PNAS)