Solution Overview

To solve this, we will utilize the well-known function collect, alongside the lesser-known as_coefficients_dict. First, we define our expression and variables:

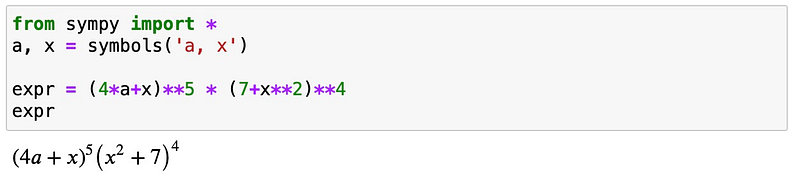
Next, we need to expand the expression:

Following this, we collect the terms based on the powers of ( x ):

While we could manually extract the coefficient of ( x^n ), it's beneficial to do this programmatically. By using as_coefficients_dict, we can create a mapping of each power of ( x ) to its corresponding coefficient:

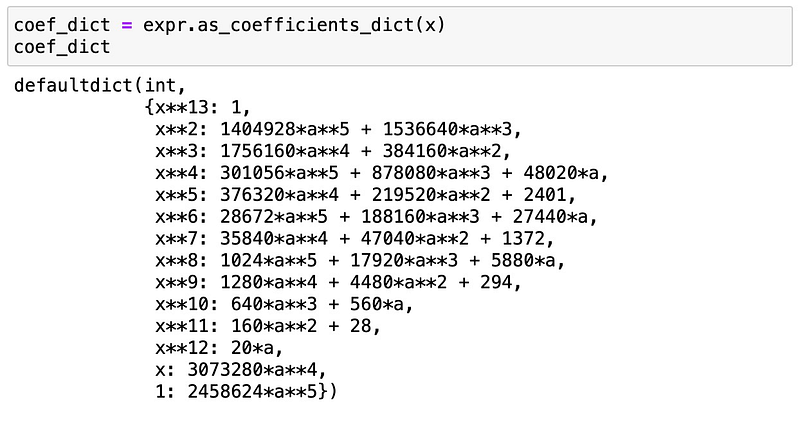
To retrieve the coefficient for ( x^n ), we simply use:

Now, let’s separate the even and odd powers of ( x ). We start with the even powers:

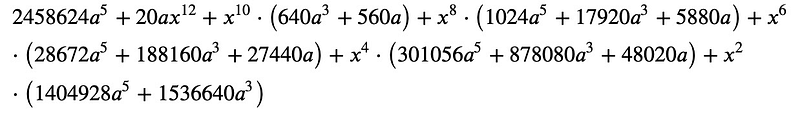
Next, we will identify the odd powers:

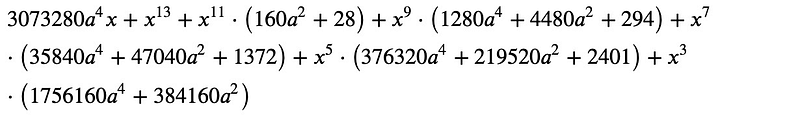
Finally, we can rewrite the odd powers using the expand and collect functions:

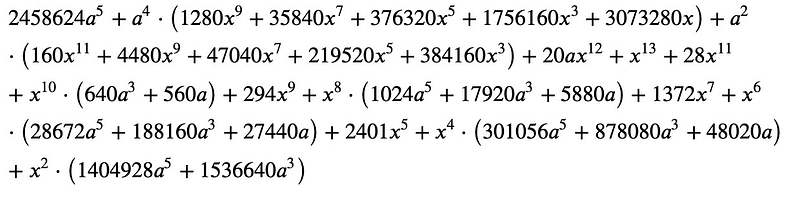
While this scenario may seem theoretical, mastering term manipulation is crucial for anyone working with algebraic expressions. Understanding these essential functions will significantly enhance your problem-solving abilities.