Unraveling the Three 3s Challenge: A Unique Math Puzzle
Written on
Chapter 1: Introduction to the Three 3s Puzzle
I recently encountered a captivating mathematical puzzle known as the Three 3s Problem. Initially, as I delved into it, the challenge seemed simple and somewhat monotonous. However, I soon discovered an unexpected twist that changed my perspective entirely. This intriguing problem is definitely worth sharing, which brings us to this exploration.
For the purpose of clarity, I've adjusted the original rules to simplify the mathematics and enhance accessibility. Let's dive into the game's regulations.
The Rules of the Three 3s Problem
The rules are straightforward. Your task is to complete a set of ten equations using only the number three, manipulating it with various mathematical symbols.
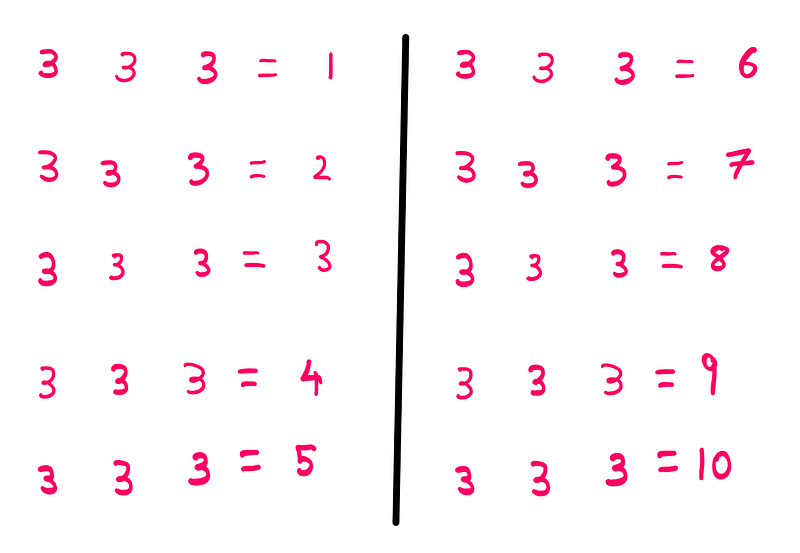
You are permitted to use the following operations: parentheses ( ), addition (+), subtraction (–), multiplication (*), division (/), and factorial (!). Now that you are familiar with the rules, I will demonstrate how to solve what is arguably the simplest equation in the set. After that, you can attempt the remaining equations independently.
Sample Solution for the Three 3s Problem
The ninth equation, which aims for a result of '9', is considered the easiest to solve. By adding '3' to itself three times, you arrive at '9'. Therefore, you only need to place two plus signs in the equation:

With this example in hand, I encourage you to take a break from this article and tackle the other equations on your own.
Challenge Alert: The tenth equation is particularly tricky and may require considerable time and effort.

If you find yourself stuck, don’t hesitate to return here for the solution.
Spoiler alert: From this point onward, I'll reveal explicit solutions to the equations.
The Remaining Solutions
I typically tackle such problems by starting with the easier ones, so let's work on the equations involving '3', '6', '2', and '4'. These can be solved quite easily as follows:
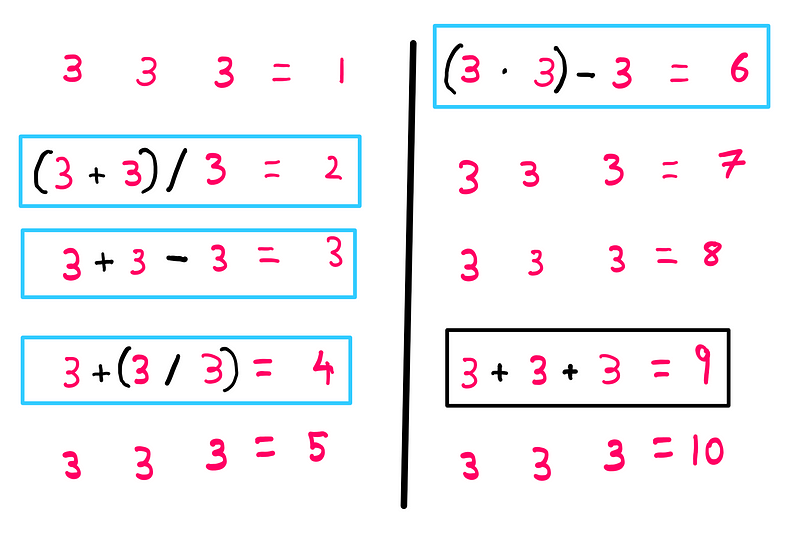
It’s important to note that the solutions presented here are not the only possibilities; there are various ways to arrive at the answers.
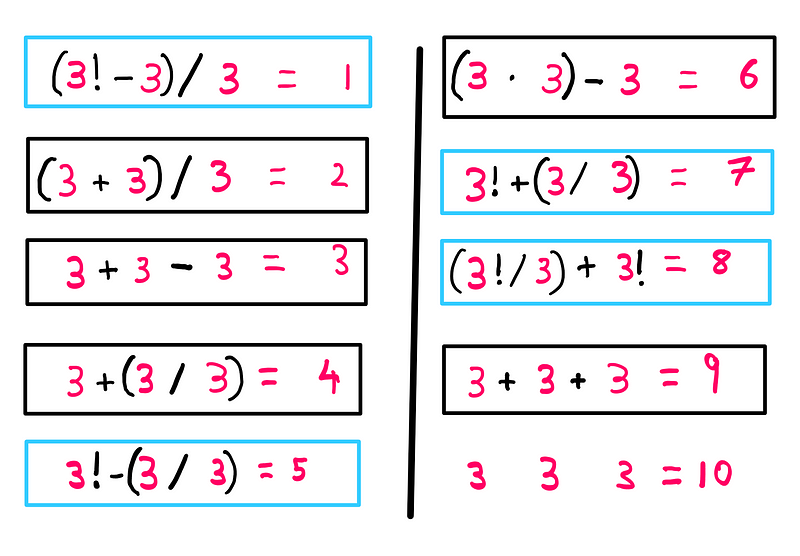
Equations involving '1', '5', '7', and '8' can be tackled using the factorial function:
Chapter 2: The Final Challenge
Now we reach the final challenge—the equation that results in '10'. As I mentioned earlier, this one took me hours to crack. The solution is not only counterintuitive but also involves a concept that many may not be familiar with. I will present the solution first and then explain the underlying principle.

This unconventional solution raises questions. What is the exclamation mark doing in front of a number? Is this even valid? To clarify, we need to understand the subfactorial function.
Understanding the Subfactorial Function
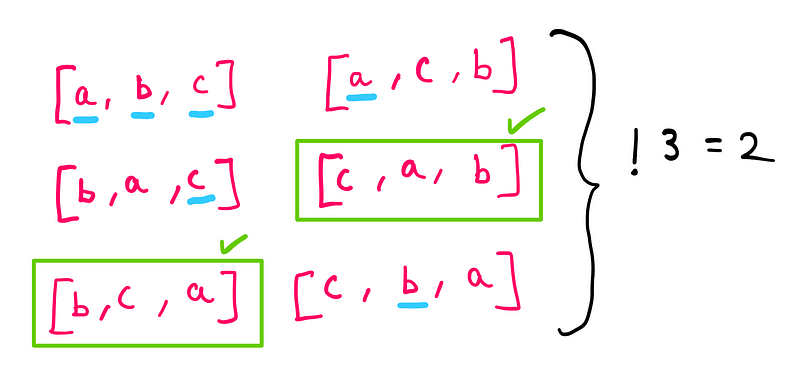
In combinatorics, the factorial function counts the permutations of a set of distinct items. For example, 3! indicates the number of arrangements of three items. Let's revisit our example of three items—let's say a, b, and c.
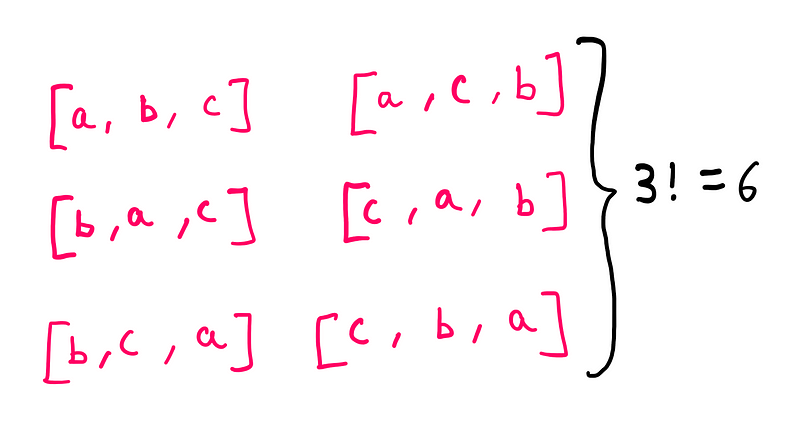
Conversely, the subfactorial function counts the derangements, or arrangements where no item appears in its original position. For three items, !3 calculates how many ways we can arrange them without any item returning to its original spot.
The formula for the subfactorial function is:
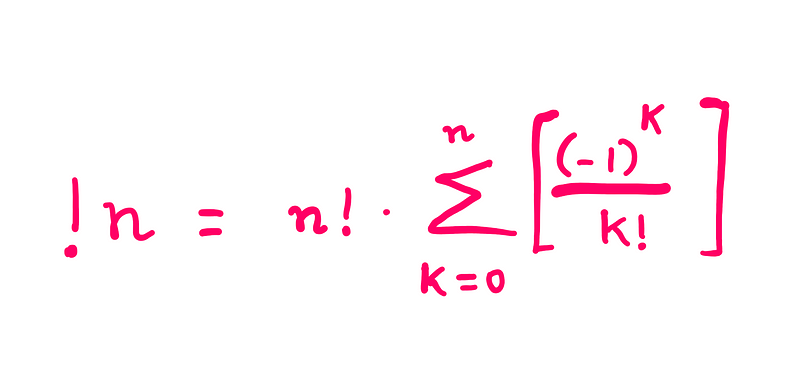
By utilizing the subfactorial function, we adhere to the game's rules while achieving an equation that equals 10.
Acknowledgments and Final Thoughts
It's refreshing to uncover a novel mathematical function hidden within a seemingly simple puzzle. I extend my gratitude to Carl Ho for creating this brilliant challenge. Although the original puzzle allowed for greater mathematical flexibility, I opted for stricter rules to make it more approachable.
It's worth mentioning that '10' is indeed a special case. Solving it without knowledge of the subfactorial function is quite difficult. If you feel a bit misled, remember that mathematics can often present such surprises. The silver lining is that we gain valuable insights from these challenging experiences.
In many cases, the approach to solving puzzles is more important than the solutions themselves. If you've discovered interesting methods to tackle these puzzles, please share your insights in the comments!
I hope you found this exploration engaging and informative. If you'd like to support my work, consider clapping, following, and subscribing for more content.
Further reading that may pique your interest: How to Solve the Doubling Puzzle? and How to Effectively Use Mathematical Induction?
This engaging video titled "Can You Solve The Three 3s Challenge?" explores the intricacies of this fascinating puzzle and its various approaches.
In this informative video, "Make 1-9 with only three 3s," viewers are guided through creative solutions and insights related to the Three 3s Problem.