The Unique Properties of Three-Dimensional Space and Motion
Written on
Prologue: Unraveling the Mysteries of Three Dimensions
In our previous discussion, we uncovered the remarkable and specific nature of three-dimensional geometry, which uniquely permits the concept of "perpendicular" or "right-angled" planes. We also touched on how rotations are defined through an axis and an angle—a phenomenon that is exclusively valid in three dimensions. Now, let’s delve deeper into the definition of a rotation, while also reviewing some foundational theories about linear operators that will aid in this exploration.
Three-Dimensional Geometry: A Complex Interplay
The peculiarities and coincidences in three-dimensional space often lead to confusion in understanding three-dimensional geometry.

Rotation Lie Groups
As established earlier, a rotation is characterized as a homogeneous proper orthogonal linear transformation. This means that its inverse corresponds to its transpose, and the determinant of its matrix equals +1. When we extend these concepts into complex vector spaces, we utilize the Hermitian conjugate, which is akin to the complex conjugate transpose. In complex vector spaces, these transformations are referred to as "unitary," but essentially, they share the same properties.
An interesting observation is that the product of two such transformations remains a homogeneous proper orthogonal linear transformation, as does the inverse of any such transformation. Thus, the collection of rotations within a specified dimension forms a matrix group known as the matrix Lie Group SO(N) (with "SO" denoting "special orthogonal," where "special" indicates that the determinant is unity, a feature preserved through matrix multiplication and inversion).
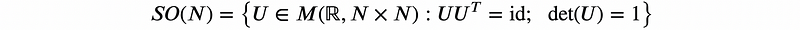
The Lie Algebra of this group corresponds to the tangent space at the identity—essentially the vector space of all directional derivatives at the identity within the group. For SO(N), this is represented as:
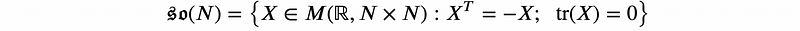
Can you verify this? A hint: consider an element "close" to the identity represented by the matrix T=id+?X. By definition, it must satisfy (id+?X)(id+?X) = id and det(id+?X) = 1. Now compute the directional derivative d/? (id+?X)(id+?X) to establish that X = -X? and apply Jacobi's formula for the derivative of a determinant to conclude that the matrix must be traceless.
Furthermore, it is noteworthy that SO(N) is topologically compact, which implies (without proof here) that the exponential function maps the group's Lie Algebra ??(N) onto the entirety of SO(N). Currently, as of 2023, the question of when exp is a surjective mapping in Lie Groups remains an open research topic. However, it is established that compactness guarantees surjectivity for compact, connected Lie Groups, leading to a comprehensive statement:
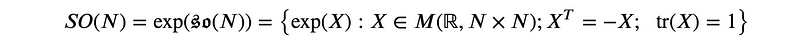
Understanding Angular Velocity
A rotation operator can be expressed in the form exp(X(t)), where X(t) = -X(t)? is a time-dependent matrix that belongs to the Lie Algebra of skew-symmetric real matrices. By the definition of the Lie algebra, we can always represent the time derivative of the rotation operator exp(X(t)) as follows:
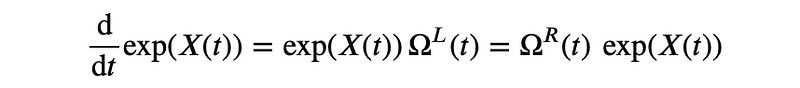
where ??(t) and ??(t) represent the left and right translated Angular Velocity Two-Forms. While they belong to the Lie algebra as skew-symmetric N×N matrices, they are generally not equal to each other or to X(t) unless the group member exp(X(t)) follows a geodesic path.
In general, we consider X(t) as a superposition of Lie Algebra basis vectors (all skew-symmetric N×N matrices for SO(N)):
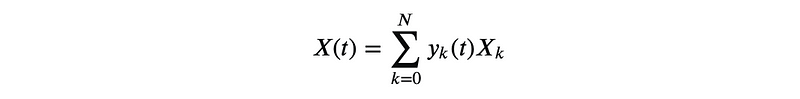
Employing the Schur-Poincaré identities:
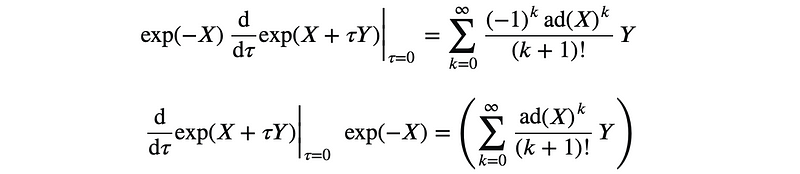
we can derive the total derivative in terms of the y?(t) coordinates, thus demonstrating:
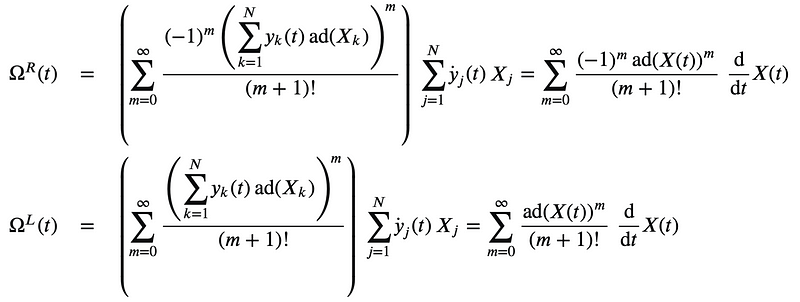
In SO(N), all operators are exponentials of Lie Algebra members. In some non-compact Lie groups, like the Lorentz Group, this exponential relationship holds only for operators within a certain proximity to the identity. Hence, we can always utilize the standard expression for the derivative of exp to formulate the angular velocity two forms as indicated above.
To distinguish between the two angular velocity two forms, we can take the transpose of the equation for ??(t) and apply the identity (ad(X)Y)? = [X,Y]? = [Y?,X?] = -ad(X?)Y?. Noting that the Lie Algebra comprises skew-transpose matrices for SO(N), we conclude that (ad(X)Y)? = -ad(X?)Y? = -ad(X)Y, and thus (ad(X)?Y)? = (-1)?ad(X)?Y. Therefore, the two forms are transposes of each other:
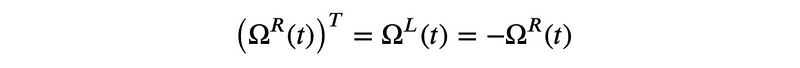
This aligns with the Group Action of SO(N) on column vectors, which represent position vectors. When the group member acts on the position vector Y from the right, we must transpose the position vector into a row vector to obtain the velocity, expressed as a row vector: V? = Y???(t). Transposing yields: V = ??(t)?Y = ??(t)Y, which correctly represents the group action on the left.
The significance of the Angular Velocity Two Form is that it serves as a linear map that connects a position, relative to the stationary point within the rotation plane, to the instantaneous velocity of that point in the rotating frame. Therefore, angular velocity can be characterized as a rank 2 tensor that transforms position vectors into velocity vectors.
To illustrate the construction of an angular velocity matrix as a two form, consider a rotation transforming a vector Y with time-dependent variation. The angular velocity two form can be expressed as:
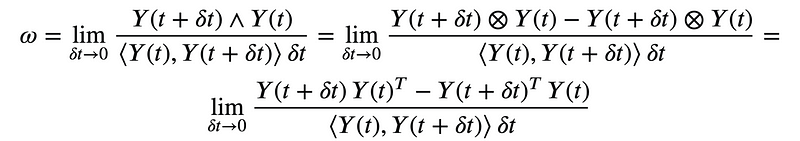
Consequently, the instantaneous velocity of the point at position Y is given by V = ? Y, where ? is the N×N matrix discussed earlier, and Y is the N×1 column vector that denotes the position.
The Spinor/Quaternion Form of Angular Velocity: A Simplified Approach in Three Dimensions
In three spatial dimensions, the rotation group can also influence the Lie Algebra ??(2)???(3) of purely imaginary quaternions through the spinor map, which embodies rotations in the double (universal) covering SU(2):
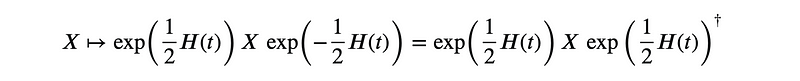
Utilizing the techniques previously discussed, taking the time derivative yields:
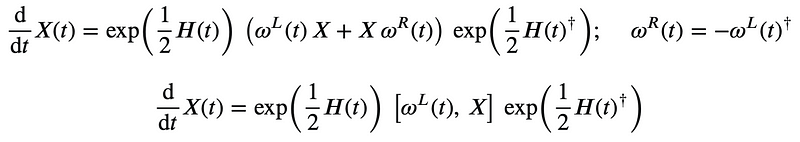
where the angular velocity two forms ? operate on the pure quaternions using Lie Brackets. The pure quaternions represent the Lie Algebra ??(2) of SU(2), allowing us to express the velocity V in terms of the position X relative to the center of rotation within the rotating frame:
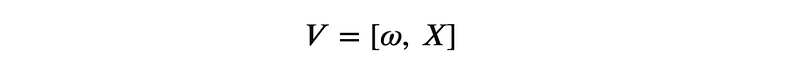
This implies that our position "vectors" are now represented as 2×2 matrices, equivalent to pure quaternions. The Hodge Star operation transforms position vectors into two forms in three dimensions:
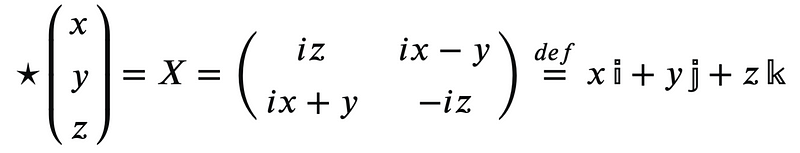
The Hodge Star (Hodge Dual) is always involute (self-inverse), meaning that the star of the matrix on the right corresponds to the column vector on the left, enabling us to conduct our operations. The pure quaternions form the Lie Algebra ??(2)???(3) and it is straightforward to verify that the four-dimensional number:
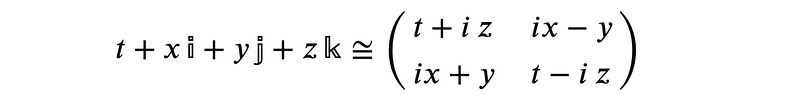
is a matrix representation of quaternions that is isomorphic to the quaternions themselves. This representation, attributed to the 19th-century mathematician J. J. Sylvester, builds upon the work of William Rowan Hamilton and generalizes complex numbers and their real-valued 2×2 matrix representation, which I previously introduced.
Imaginary Numbers and Their Practical Applications
The quaternion skew-field representation is uniquely effective in three dimensions, making it an invaluable tool for analyzing rotational systems—another fascinating property of three-dimensional space. Notably, any pure quaternion (one devoid of a real part) squares to a real number:
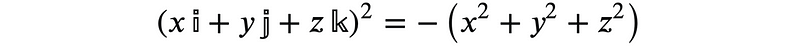
Exponentiating a pure quaternion to the Lie group SU(2) of unit quaternions results in:
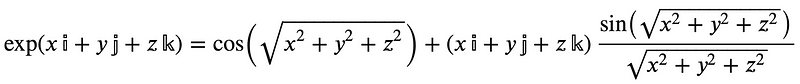
For a general quaternion, the real number t commutes with any quaternion, yielding:
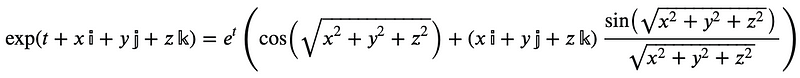
Thus, quaternions can be considered as the direct product of the Group of Positive Reals and multiplication with the unit sphere quaternion. The logarithm of a general quaternion can be determined as follows:
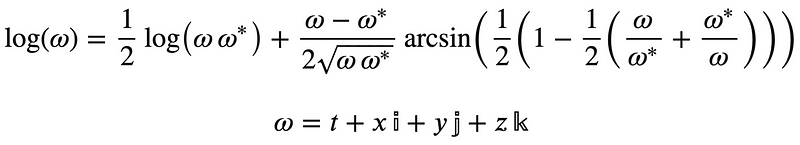
Chapter 3: Exploring Higher Dimensions
This video titled "The things you'll find in higher dimensions" explores the fascinating concepts and phenomena that emerge when we extend our understanding beyond the conventional three-dimensional space.
Chapter 4: Visualizing the Fourth Dimension
In this video titled "Categorical Mental Imagery: Visualizing the 4th Spatial Dimension" with Jim Zhong, viewers will learn about the visualization techniques and mental imagery related to the complexities of the fourth dimension.