# Understanding the Quotient Rule in Calculus
Written on
Introduction to the Quotient Rule
This article marks the tenth installment in our calculus series, focusing on the foundational concepts behind the quotient rule in differentiation. In the previous discussion, I examined the product rule. Now, we will build upon that knowledge.
Let’s consider two functions defined as follows:
u(x) = 6x² + a
v(x) = 2x + b
y(x) = (6x² + a)/(2x + b) = u/v
dy/dx = ?? [where a and b are constants]
As with our earlier exploration, u(x) and v(x) are distinct functions of the variable ‘x’. We derive y(x) by dividing u(x) by v(x). The pressing question is: how can we compute the derivative dy/dx? Let's delve into this.
Intuitive Approach to Finding dy/dx
In the previous analysis, we used an intuitive method when y(x) was the product of u(x) and v(x). We first differentiated u(x) with respect to ‘x’ and then v(x) in a similar manner. Finally, we multiplied these derivatives to find dy/dx.
However, this method does not lend itself well to division, as it is unclear how to divide the numerator by the denominator. Thus, we must adopt a different approach based on first principles.
Applying First Principles to Derive the Quotient Rule
Following our previous methodology, let’s increase ‘x’ by a tiny increment, ‘dx’. Accordingly, ‘y’ increases by ‘dy’, ‘u’ by ‘du’, and ‘v’ by ‘dv’ (where ‘dy’, ‘du’, and ‘dv’ are infinitesimally small). The updated expression is as follows:
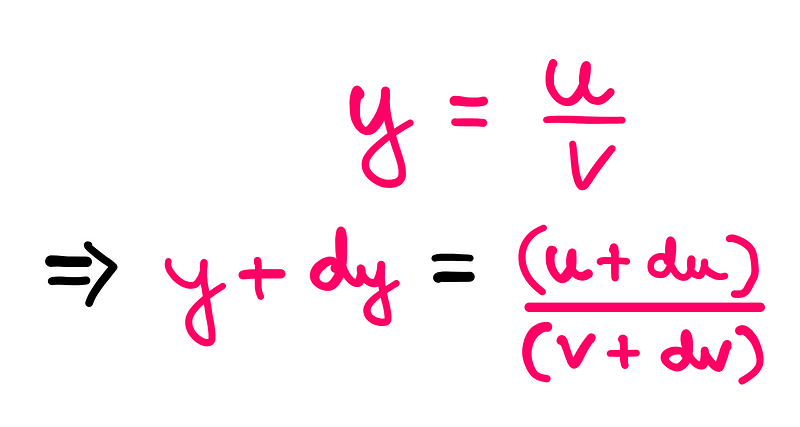
Now, we can simplify the right-hand side of the equation by employing algebraic division (specifically, polynomial long division):
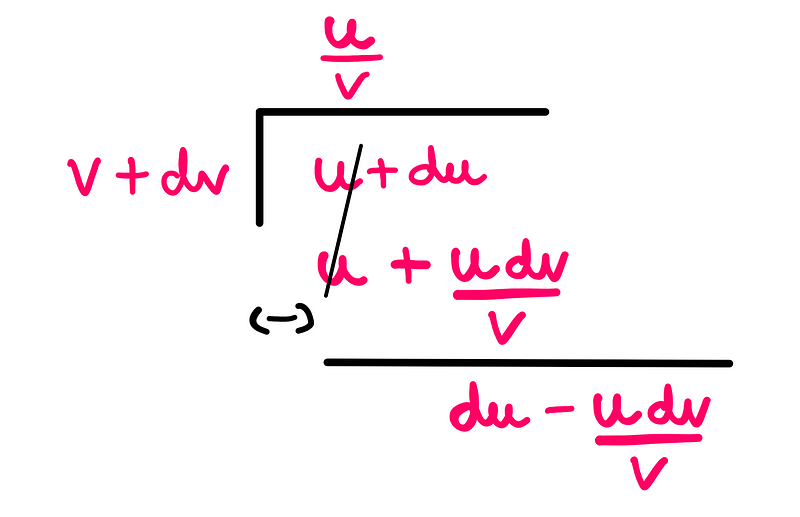
Continuing this division method, we can resolve subsequent remainder expressions:
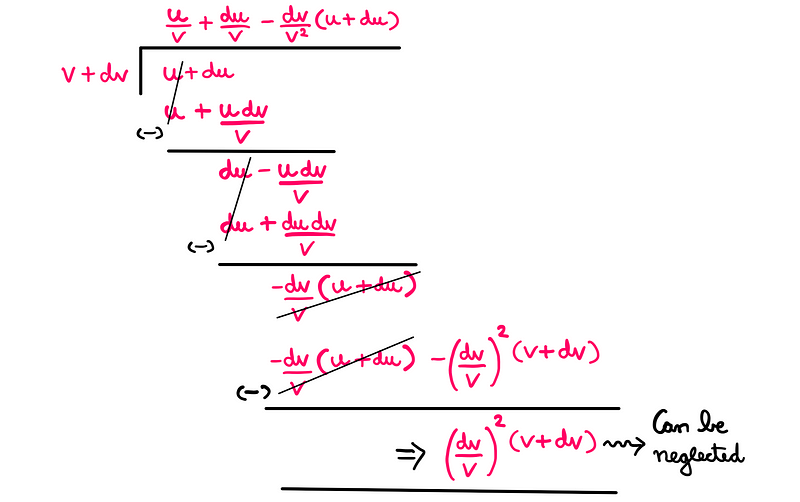
The last term in the remainder is of second-degree smallness, allowing us to disregard it and focus on the quotient as our solution. Let’s continue simplifying the expression derived from the quotient:

This results in the final expression which articulates the quotient rule of differentiation.
Interpreting the Quotient Rule
Here’s a concise step-by-step overview of how to implement the quotient rule:
- Multiply the denominator by the derivative of the numerator.
- Multiply the numerator by the derivative of the denominator.
- Subtract the result from step 2 from the result of step 1.
- Divide the final result by the square of the denominator.
Now, let’s apply this understanding to our initial example:
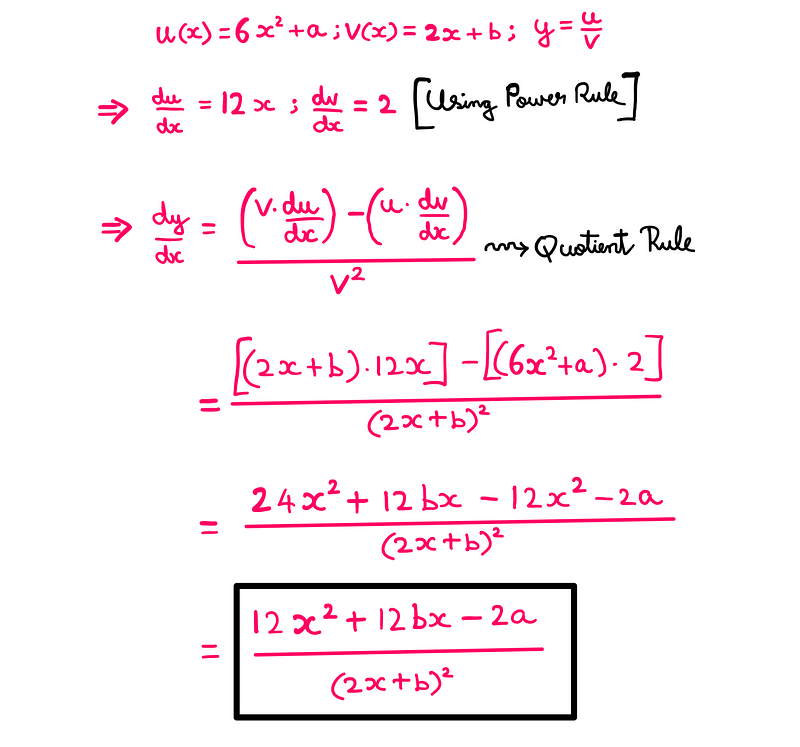
We have effectively utilized the first principles to grasp and execute the quotient rule of differentiation.
Next Steps in Our Series
Moving forward, I plan to tackle additional example problems to reinforce the concepts discussed thus far.
Quotient Rule for Derivatives - This video provides a clear explanation of the quotient rule, showcasing its application and significance in calculus.
Calculus: The Quotient Rule for Derivatives - In this video, the quotient rule is explored in detail, making it easier to understand how to differentiate functions involving division.
If you appreciate this content and wish to support future projects, consider contributing on Patreon.
Reference and credit: Silvanus Thompson.
You can read the original essay here.