Understanding the Physics of Water Balloons Using Python
Written on
Chapter 1: Introduction to Water Balloon Physics
In this section, we delve into the physics of a water balloon thrown at an angle, analyzing its trajectory and calculating its velocity. This scenario falls under the realm of mechanics, specifically kinematics. I will utilize a playful example from a math and physics textbook to derive the motion equations and visualize them using Python.
Problem Statement
Consider the following problem: “You launch a water balloon from ground level at an initial speed at an angle θ above the horizontal. Determine the balloon's velocity at different points in its trajectory, specifically the vertical component of velocity as a function of time, when considering both upward and downward directions.” — Savov (2016, p. 238)
This classic kinematics problem, which incorporates elements of calculus, will be solved both manually and through Python programming. I will start by deriving the motion equations from a sketch I created and subsequently plot the velocities for various θ values.
Kinematics Equations
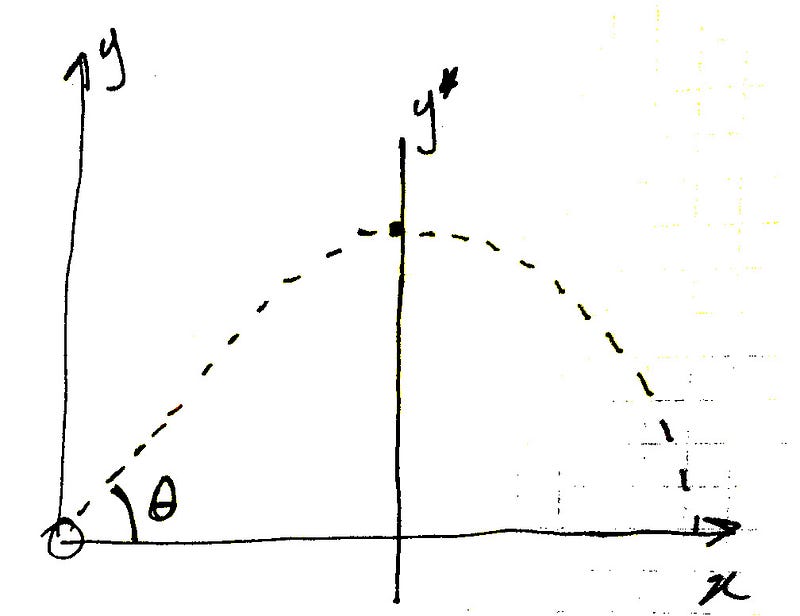
To visualize the problem, refer to Figure 1, which illustrates the scenario described:
In classical physics, the connection between force, acceleration, velocity, and displacement is expressed by the following equation:
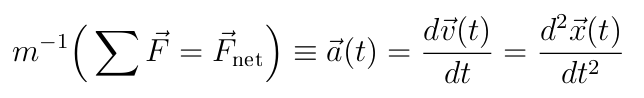
This equation separates the forces acting on an object (left side) from the object's motion (right side). In this case, I will focus on defining acceleration based on this graph, rather than analyzing the forces affecting it.
The water balloon is projected from the origin at angle θ. When analyzing the motion concerning the vertical axis, the sine function comes into play. Equation 2.1 provides the acceleration function for the water balloon:
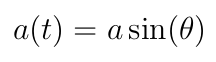
Here, -g represents the gravitational acceleration in kinematic equations. Incorporating this, Equation 2.2 is formulated:
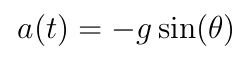
From the initial equation, we recognize that an object's acceleration is the derivative of its velocity, while velocity is the derivative of its displacement. Given that I only have the acceleration, I will apply anti-derivatives to derive both the velocity and displacement functions from Equation 2.2. Equation 3.1 illustrates the resulting velocity function:
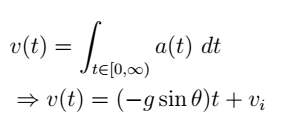
Similarly, the displacement function can be derived from the velocity function, represented by Equation 3.2:
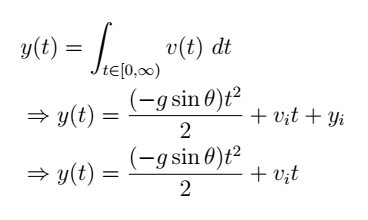
I omitted the initial vertical position since the balloon is launched from the ground (i.e., y₀ = 0). The problem also queries the kinematic equations under an unusual scenario where gravity acts upward. These equations can be derived by reversing the signs of the gravitational and initial velocity coefficients in Equations 3.1 and 3.2.
To verify the results, I used the Sympy Live Shell, as shown in Figure 2:

It's important to note that Sympy does not automatically include the constant of integration, so I had to add that manually. Additionally, I avoided specifying concrete units (like meters or seconds) to simplify the problem as an abstract mathematical exercise.
Visualisation
To visualize the derived kinematics equations, I employed Python and Matplotlib. I began by launching Jupyter Notebook and importing the necessary libraries:
import math
import numpy as np
import matplotlib.pyplot as plt
Next, I implemented the displacement function I derived:
def y(t, θ):
y = -9.81 * math.sin(math.radians(θ))
y = y * t**2 / 2.0 + 10 * t
return y
Using a gravitational constant of 9.81 and an initial velocity of 10, I set the plotting range and defined angles for visualization:
R = np.arange(0, 10, 0.01)
angles = [
[15, "red"],
[25, "purple"],
[35, "green"],
[45, "blue"]
]
I then set up the plot and visualized each angle:
plt.figure()
plt.rcParams['xtick.bottom'] = plt.rcParams['xtick.labelbottom'] = False
plt.rcParams['xtick.top'] = plt.rcParams['xtick.labeltop'] = True
for k in angles:
plt.plot(R, [y(t, k[0]) for t in R], color=k[1], label=str(k[0]) + " deg.")
plt.legend()
plt.grid()
plt.title("Water Balloon Trajectory Over Time", fontsize=16)
plt.ylabel("Vertical Position y(t)", fontsize=16)
plt.ylim(0, 25)
plt.xlim(0, 8)
plt.show()
Figure 3 illustrates the resulting kinematics plot:
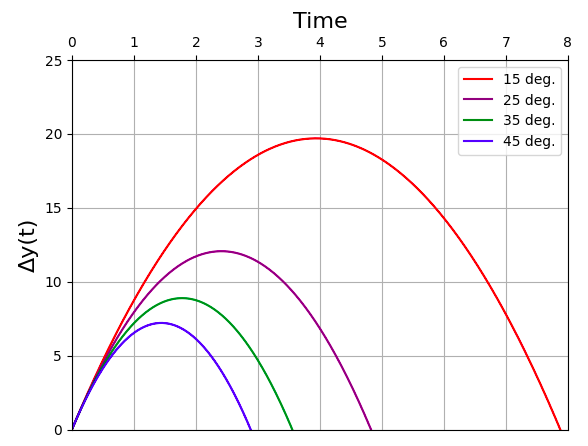
Chapter 2: Video Demonstrations
To further understand the physics behind water balloons, consider these video resources that provide visual explanations.
The first video titled "Science of Water Balloons" from @sixtysymbols explores the principles of physics at play:
The second video, "The Physics of Popping Water Balloons," delves into the mechanics involved when a water balloon bursts:
Conclusion
This exercise illustrates a fundamental physics problem commonly encountered by computer science and physics students alike. While my solution may have its flaws, such as not using standard units, I believe it effectively demonstrates how Python can be utilized for basic computational physics.
References
Savov, I. (2016). No Bullshit Guide to Math & Physics. Minireference Publishing.