Navigating Projective Geometry and Information Theory for Mars Missions
Written on
Chapter 1: Understanding Projective Geometry
In my earlier article discussing the intersection of projective geometry and information theory, I introduced concepts surrounding error-detecting and error-correcting codes. After successfully landing your Martian vehicle, you attempted to send an error-corrective signal to adjust the course of your wayward Mars drone.
We delved into the relationship between the Hamming code and the Fano plane, but as your drone rushed toward a Martian boulder, I left you hanging. In this piece, we will clarify these concepts further, addressing the connection between the Hamming code and the Fano plane while devising a strategy to rescue your drone.
If you haven't yet read the first essay, I strongly recommend doing so, as this discussion builds upon those principles. Let's dive in!
Section 1.1: Analyzing the Fano Plane
First, let's break down the Fano plane and examine its components. As mentioned previously, the Fano plane consists of seven points and seven lines, including a curved line. In the following illustration, you will notice that I've assigned numbers to the points from 1 to 7:
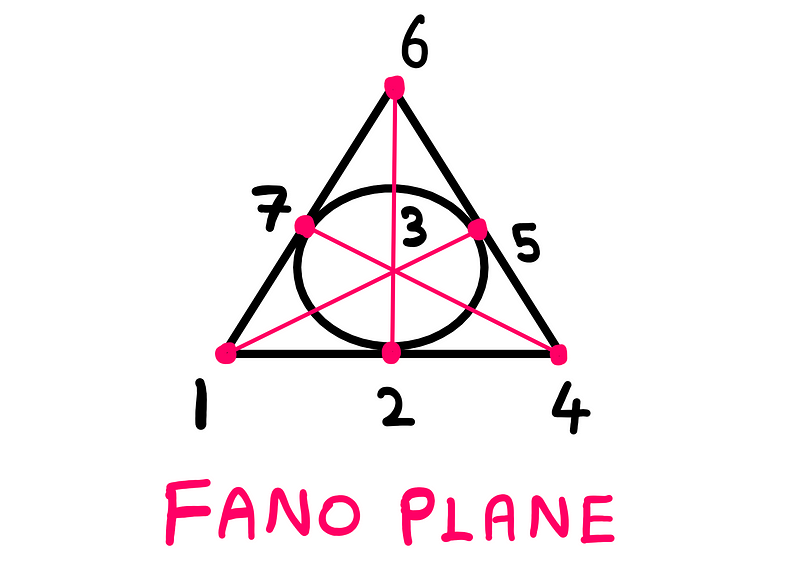
The Fano Plane — Illustration created by the author
With this numbering in mind, you can see that each line in the Fano plane can be expressed using three points. Below is the list of all the lines:
- 124
- 135
- 167
- 257
- 347
- 236
- 456
Now that we have this list, let’s turn our attention to the Hamming code.
Section 1.2: Relating the Fano Plane to the Hamming Code
In my earlier essay, I discussed how Richard Hamming, a colleague of Shannon at Bell Labs, developed the Hamming code. I also outlined the Hamming code combinations for any three-digit binary setup:
- 000 → 0000000
- 001 → 0010111
- 010 → 0101011
- 011 → 0111100
- 101 → 1011010
- 110 → 1100110
- 100 → 1001101
- 111 → 1110001
Now, let’s transform the list of Fano lines into binary code. Instead of a direct conversion, I will apply specific logic. Let “xxxxxxx” represent the binary code for any line in the Fano plane. The 'x' on the far left indicates point number '1,' while the 'x' on the far right denotes point number '7.' If a point 'x' is present in a line, we replace it with a '0'; if absent, we substitute it with a '1.'
This leads to the following binary representations of Fano lines:
- 124 → 0010111
- 135 → 0101011
- 167 → 0111100
- 257 → 1011010
- 347 → 1100110
- 236 → 1001101
- 456 → 1110001
Notice how, aside from the absent point (0000000), this binary list matches the Hamming code. What motivated Hamming to select these specific numbers? Let’s investigate.
Chapter 2: The Intersection of Projective Geometry and Information Theory
As a reminder, Richard Hamming aimed to create a self-correcting information transmission system capable of addressing any corruption or errors in the data.
Imagine you send a corrective signal to your Mars drone using the Hamming code, structured as follows:
10101 → 010 101 → 0101011 1011010
Hamming's greatest fear was a bit flip that could mistakenly convert one code into another. In your corrective signal, there are two adjacent Hamming code blocks. How many bit flips would it take to change one block into the other?
The answer is four. This exemplifies Hamming’s brilliance; while others overlooked the geometric aspects of binary signals, he recognized their significance. He introduced the concept of Hamming distance, which measures how many bit flips are needed to convert one Hamming code block into another. By examining Hamming's code list, you will find that any two blocks are separated by a minimum of four units of Hamming distance.
While neither Gino Fano nor Richard Hamming intended for their work to converge, subsequent mathematicians have identified the connection between Hamming codes and projective planes. Such discoveries often lead to innovative developments. Interestingly, this link was exploited by MIT students to successfully manipulate a state lottery, netting them millions.
You might wonder, “Why consider lotteries when my Mars drone is about to crash?” Let’s stay focused on the task at hand—saving your drone!
Section 2.1: Strategies to Rescue Your Mars Drone
The Hamming Code operates using a linear error-correcting algorithm, capable of detecting two-bit errors and correcting one-bit errors. This is suitable for applications like ECC-RAM (Error Correcting Code — Random Access Memory), but what about your Mars drone?
Without delving into more advanced error-correcting codes, here are two potential strategies:
- The Hamming code we’ve discussed employs (2^r — 1) bits, where r=3. Increasing the value of r will enhance redundancy, thereby lowering the chances of signal corruption. However, be mindful that this will also reduce transmission speed.
- You could replicate the Hamming code signal three times and instruct the drone to return a copy of the input signal. If it matches, you can send a concise confirmation signal for the drone to execute the necessary corrective action.
The critical takeaway here is that while error-correcting codes can significantly reduce the likelihood of signal corruption, they cannot entirely eliminate it. Depending on your needs—for instance, if speed is paramount—you’ll have to make a decision and hope for a favorable outcome.
Chapter 3: Conclusion and Next Steps
To simplify the nature of the challenge: imagine organizing a party where your goal is to invite as many guests as possible while ensuring that each guest is as far apart as possible. Projective geometry proves to be a valuable tool for addressing this issue. The Fano plane has aided us in understanding the Hamming code, but in practice, mathematicians and scientists often utilize higher-dimensional geometries for more complex algorithms.
Closing Remarks
When Richard Hamming invented the Hamming code, Bell Labs perhaps recognized its significance more than Hamming himself. The lab resisted Hamming’s attempts to patent his creation. Ironically, Swiss mathematician Marcel Golay learned about Hamming's ideas from Shannon and developed his own variations of error-correcting codes, publishing first, which sparked an ongoing debate over credit for the invention.
Ultimately, due to an antitrust settlement, Bell Labs lost the right to charge for licenses on Hamming codes anyway.
Epilogue
As your drone hurtles toward the Martian rock, you prioritize signal speed and opt for the standard 7–4 Hamming code (the one we just discussed), hoping for a successful outcome.
With mere seconds remaining, your drone receives the correct transmission and survives to explore another Martian day, heading toward Mount Olympus, its intended destination.

You exhale with relief, acknowledging the role of chance and randomness in the process. All you could do was minimize the likelihood of error or corruption while seeking the fastest possible transmission.
Reference and credit: Jordon Ellenberg and Patrick Fleming.
If you appreciate my work, consider clapping, following, and subscribing.
Further reading that might pique your interest:
- How To Really Solve This Packing Spheres Puzzle?
- How To Perfectly Predict Impossible Events?
- How To Actually Solve The Königsberg Bridge Problem?
If you'd like to support future content, consider contributing on Patreon.
You can access the original essay here.
The first video titled "Projective Geometry 2 Foundations & Tilings in Perspective" explores the foundations of projective geometry and its application in perspective tiling.
The second video titled "Projective Geometry | Math History | NJ Wildberger" delves into the historical context and developments in projective geometry.