Chapter 1: Introduction to Heisenberg Spin Chains

Understanding the low-energy configurations within a sequence of atoms is crucial in the study of quantum mechanics.

Motivation

There is a significant amount of research in the field of physics focused on the mechanisms of magnetism. Contemporary theories regarding magnetism hinge on the atomic spin within materials and their interactions. Given our understanding of atomic behavior at microscopic levels, it's no surprise that these models are rooted in quantum mechanics. This framework suggests that the system doesn't exist in a singular state; instead, it represents a linear combination of potential states that manifest with specific probabilities upon repeated measurements.

The quantum mechanics governing multi-particle systems can be exceedingly complex. To enhance our comprehension of these systems, we can simplify by analyzing a one-dimensional array of atoms that exhibit magnetic properties, which leads us to the exploration of quantum spin chains. A spin chain serves as a theoretical representation of atoms arranged in a lattice, where they interact based on their spins.

Let's illustrate this with a fundamental example: when adjacent atoms are aligned with opposing spins, they might incur an energy cost that incentivizes them to align in the same direction. There are intriguing questions in quantum mechanics regarding the energy levels and configurations of such systems. Each 'site' within this chain is associated with a specific set of states, referred to as Hilbert space. The variety of states at each site is contingent upon the particle's spin. For instance, an electron possesses two spin states—up and down—resulting in a linear combination of these states at a given site. When multiple sites are connected in a chain, the overarching Hilbert space is represented as the tensor product of these individual sub-Hilbert spaces.

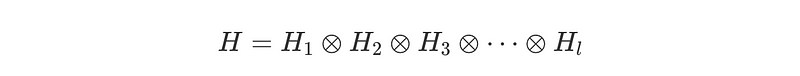
What exactly do the states within this Hilbert space resemble? They are constructed as superpositions of basis states, a possibility afforded by the linear nature of Schrödinger’s equation. A viable basis could consist of the combinations of up and down states across each site. The dimension of a Hilbert space is defined by the number of elements in its basis, a number that remains constant regardless of the chosen basis.

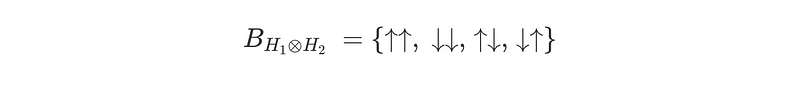
States may also exhibit entanglement. For example, the configuration of a two-site spin chain could be characterized as a superposition of two up states and two down states. This scenario demonstrates entanglement, as measuring the first state would immediately inform us of the spin direction of the second atom. Alternative bases could also consist of entangled superpositions of these states.

Chapter 2: The Heisenberg Spin Chain Model

In this section, we will delve into the specifics of contemporary spin chain models. The energy of any quantum system is governed by its Hamiltonian. A spin chain models a configuration of atoms that interact with their neighboring atoms along a chain, based on their respective spins. To clarify which operators affect which spaces, I will explicitly state the operators involved. The Hamiltonian can be expressed as a sum of spin terms, each acting on pairs of adjacent sites within the chain. Below is a simple example of a Hamiltonian for a three-atom system.

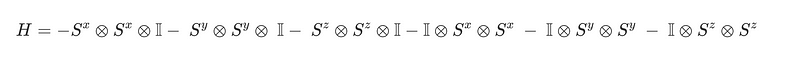
To determine the energy of this configuration, we analyze the Hamiltonian of the leftmost site initially and incrementally construct the full Hamiltonian while tracking the eigenvalues. This iterative process involves continuously updating the edge states. The methodology for building the Hamiltonian will be discussed in the subsequent section.

Combining Hamiltonians

Locating the ground state of such a system poses a significant challenge due to the extensive search space of possible states. Therefore, we turn to effective numerical methods. Techniques such as the DMRG method allow us to derive the ground state iteratively, beginning with the ground state of a smaller segment of the chain and progressively adding sites.

In this model, if we possess the Hamiltonian for the first n sites, we can represent it as S_n, the spin operator acting on the nth site—the boundary of these n sites. To update this Hamiltonian to describe n+1 sites, we extend the Hilbert space by taking a tensor product with the identity to preserve the first n states and introduce an interaction between the nth and (n-1)th sites.

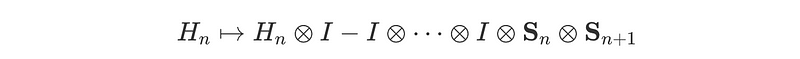
We must also adjust the boundary of the block by shifting it one site forward, achieved by performing another tensor product as follows:

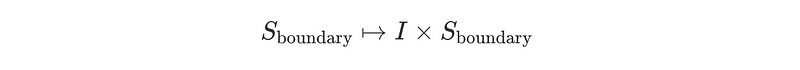
In a future article, I will elaborate on the DMRG model and its application in determining the ground state.

Video Resources

To further explore the dynamics of magnetization and Heisenberg spin chains, check out the following videos:

An insightful discussion on the dynamics of magnetization in Heisenberg spin chains from the Qiskit Quantum Seminar.

Jules Lamers presents an engaging talk on the Heisenberg spin chain and its related phenomena.