Advanced Techniques for Solving Line Integrals in Python
Written on
Chapter 1: Introduction to Line Integrals with SymPy
In my earlier Medium.com article, I discussed the process of calculating line integrals using SymPy. Recently, I encountered a function named line_integrate within SymPy that claims to accomplish this task. However, upon inspection, I found it lacked the flexibility I needed. While experimenting with this topic, I devised a more effective method that utilizes custom classes, making the evaluation of line integrals more streamlined.
To begin, similar to my previous discussion, I will compute the integral
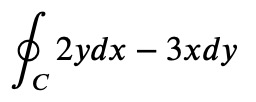
where the variable represents the unit circle. This will be accomplished using customized Python classes, and then I will apply the same classes to a contour integral
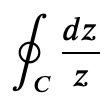
in the complex plane. The classes are designed to display themselves neatly in Jupyter notebooks. If the integration path is a closed loop, the integral sign will reflect that; otherwise, a standard integral sign will be shown.
So, grab your coffee, fire up a Jupyter notebook, and let's import SymPy:
from sympy.abc import *
from sympy import *
Chapter 2: Creating Custom Classes for Integration
Section 2.1: Defining the Contour Class
Both the line integral and the contours for integration will utilize custom classes. For instance, to define a unit circle, I will create:
circle = Path('C', t,
{x: cos(t),
y: sin(t)},(t, 0, 2*pi))
The initial argument designates a name that will appear below the integral sign in Jupyter. The second argument indicates the parameter for the path. The third is a dictionary that outlines how to parameterize the coordinates, and the final argument specifies the parameter's range.
The class constructor not only stores these parameters but also assesses whether the path is closed. My preference for list and dictionary comprehensions is evident in this implementation. Here's how to visualize the path:
plot_parametric((circle.funcs[x],
circle.funcs[y]),
circle.limits)
Section 2.2: Implementing the Line Integral Class
Now, let's delve into the implementation of the line integral itself. I aim to use it in the following way:
LineIntegral(2*y, x, circle) - LineIntegral(3*x, y, circle)
The output will resemble:
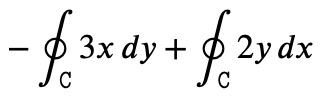
The unevaluated form will be displayed. For closed contours, the closed integral sign will be used, whereas a standard integral sign will be shown otherwise. The path's name will be indicated below the integral sign. To evaluate it, I will employ the doit() method, a common practice in SymPy:
_.doit()
This will yield:
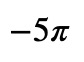
The code is crafted to allow addition, subtraction, and other standard operations with line integrals, inheriting behaviors from sympy.Expr. To ensure a unique display in Jupyter, I have overridden the _latex function.
Chapter 3: Integrating in the Complex Plane
Next, I will tackle the integral
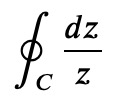
where the variable is a complex number and the integration path is a closed contour in the complex plane. For simplicity, I will once again utilize the unit circle. We can express the complex variable in terms of its real and imaginary components:
f = (1 / z).subs(z, x + I*y)
This allows us to compute:
LineIntegral(f, x, circle) + I * LineIntegral(f, y, circle)
And subsequently evaluate it using _.doit():
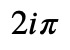
This outcome is consistent with the residues theorem. The result remains unchanged even when adding a function that lacks a first-order pole, such as:
f = (1 / z + 1 / z**2).subs(z, x + I*y)
The integral computation would be:
Ii = LineIntegral(f, x, circle) + I * LineIntegral(f, y, circle)
Ii.doit()
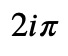
Section 3.1: Future Directions
Our custom classes have significant potential for further development. Future enhancements could include creating convenience subclasses of Path for common shapes such as lines, rectangles, and arcs. Additionally, implementing the __add__ magic method for Path could facilitate the appending of paths. However, these are ideas for future exploration, or perhaps you might experiment with them yourself! Thank you for reading!
For additional insights on utilizing Python's computer algebra package SymPy, feel free to explore my SymPy collection:
The first video titled "Integration in PYTHON (Symbolic AND Numeric)" provides valuable insights into symbolic and numeric integration techniques in Python.
The second video, "Calculus III: How to solve double integrals with SymPy and Python," offers a tutorial on solving double integrals using SymPy.